Question

Prove that set of all rational numbers is countable

Answer 1

This claim is proven by building a bijection
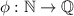`\phi: \mathbb{N}\to\mathbb{Q}` by following a diagonal procedure.

Imagine you have an infinite matrix, whose coefficient are all possible fractions:

`\left[\begin{array}{cccc}(1)/(1)&(2)/(1)&(3)/(1)&\ldots\\&&\\(1)/(2)&(2)/(2)&(3)/(2)&\ldots\\&&\\(1)/(3)&(2)/(3)&(3)/(3)&\ldots\end{array}\right]`

Now, count them "diagonally": this is how we map every natural number, using the same positions:

`\left[\begin{array}{cccc}\phi(1)&\phi(2)&\phi(6)&\phi(7)\\\phi(3)&\phi(5)&\phi(8)&\phi(13)\\\phi(4)&\phi(9)&\phi(12)&\ldots\\\phi(10)&\phi(11)&\ldots&\ldots\end{array}\right]`

The attached image, taken from aminsaied.wordpress.com/2012/05/21/diagonal-arguments/, should make it clearer