Question

Given a set s how many subsets of s contain at most 2 elements

Answer 1

Given a set S of cardinality
`n`, the subsets containing at most 2 elements are:

• The empty set
• Subsets with 1 element
• Subsets with two elements

There is clearly only one empty set, and there are
`n` subsets containing one element (you choose one of the n elements in S to create your subset)

Finally, the number of subsets containing two elements is

`\displaystyle \binom{n}{2} = (n!)/(2!(n-2)!) = (n(n-1))/(2)`

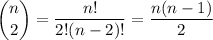
In fact, in general, the binomial coefficient
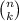`\binom{n}{k}` represents the number of subset of cardinality k that you can build from a set with cardinality n.

So, if we update our list, we have the following subsets:

• One empty set
• 
  `n` subsets with 1 element
• 
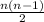  `(n(n-1))/(2)` subsets with two elements

For a total of

`1+n+(n(n-1))/(2) = (n^2+n+2)/(2)`

subsets with at most two elements.