Answer:
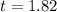
Step-by-step explanation:
Given
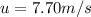 -- initial velocity
-- initial velocity
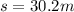 --- height
--- height
Required
Determine the time to hit the ground
This will be solved using the following motion equation.
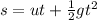
Where

So, we have:
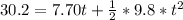

Subtract 30.2 from both sides

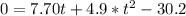
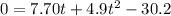
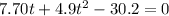
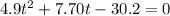
Solve using quadratic formula:
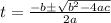
Where


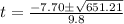
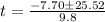
Split the expression
 or
or
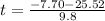
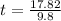 or
or
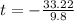
Time can't be negative; So, we have:
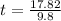
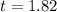
Hence, the time to hit the ground is 1.82 seconds