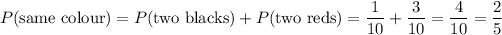Question

An urn contains two black balls and three red balls. If two different balls are successively removed, what is the probability that both balls are of the same color?

Answer 1

You can extract two balls of the same colour in two different way: either you pick two black balls or two red balls. Let's write the probabilities of each pick in each case.

Case 1: two black balls

The probability of picking the first black ball is 2/5, because there are two black balls, and 5 balls in total in the urn.

The probability of picking the second black ball is 1/4, because there is one black ball remaining in the urn, and 4 balls in total (we just picked the other black one!)

So, the probability of picking two black balls is

`P(\text{two blacks}) = (2)/(5) \cdot (1)/(4) = (2)/(20) = (1)/(10)`

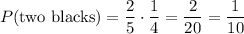
Case 2: two red balls

The probability of picking the first black ball is 3/5, because there are three red balls, and 5 balls in total in the urn.

The probability of picking the second red ball is 2/4=1/2, because there are two red balls remaining in the urn, and 4 balls in total (we just picked the other red one!)

So, the probability of picking two red balls is

`P(\text{two reds}) = (3)/(5) \cdot (1)/(2) = (3)/(10)`

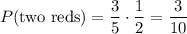
Finally, the probability of picking two balls of the same colour is

`P(\text{same colour}) = P(\text{two blacks})+ P(\text{two reds}) = (1)/(10) + (3)/(10) = (4)/(10) = (2)/(5)`