Answer:
The magnitude of her acceleration is -2.8 m/s²
Step-by-step explanation:
It is given that,
Initial velocity of the skier, u = 8 m/s
Final velocity of the skier, v = 6 m/s
Distance covered, s = 5 m
We need to find the magnitude of acceleration as she slows down. It can be calculated using third equation of motion as :
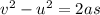
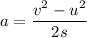
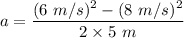
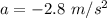
Answer:
The magnitude of her acceleration is -2.8 m/s²
Step-by-step explanation:
It is given that,
Initial velocity of the skier, u = 8 m/s
Final velocity of the skier, v = 6 m/s
Distance covered, s = 5 m
We need to find the magnitude of acceleration as she slows down. It can be calculated using third equation of motion as :
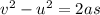
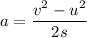
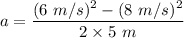
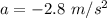
So, the acceleration of the skier is -2.8 m/s². Hence, this is the required solution.