Question

Olympic skier Tina Maze skis down a steep slope that descends at an angle of 30â below the horizontal. The coefficient of sliding friction between her skis and the snow is 0.10. Determine Maze's acceleration. Express your answer with the appropriate units.

Answer 1

Since Tina is sliding down on an inclined ramp

Net force along the inclined

`F_x = mg sin\theta`

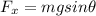
Now force component on Tina perpendicular to inclined plane

`F_y = mg cos\theta`

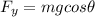
now we know that normal to the inclined plane the force is counter balanced by the normal force

So we can find the normal force as

`F_n = mg cos\theta`

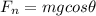
now in order to find the friction force we can write

`F_f = \mu * F_n`

`F_f = 0.10*mgcos\theta`

now along the inclined plane net force is given as

`F_(net) = mgsin\theta - F_f`

`F_(net) = mgsin\theta - 0.10*mgcos\theta`

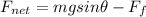
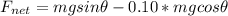
also by Newton's II law we can write

`F_(net) = ma`

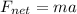
by above two equations we can write

`ma = mgsin\theta - 0.10*mgcos\theta`

`a = gsin\theta - 0.10*gcos\theta`

`a = 9.81*sin30 - 0.10*9.81*cos30`

`a = 4.06 m/s^2`

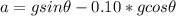
so acceleration will be 4.06 m/s^2