Question

T what point does the curve have maximum curvature? Y = 7ex (x, y) = what happens to the curvature as x → ∞? Κ(x) approaches as x → ∞.

Answer 1

Formula for curvature for a well behaved curve y=f(x) is

K(x)=
`\frac{|{y}''|}{[1+{y}'^2]^(3)/(2)}`

The given curve is y=7
`e^(x)`

`{y}''=7e^(x)\\ {y}'=7e^(x)`

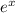
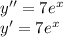
k(x)=
`\frac{7e^(x)}{[{1+(7e^(x))^2}]^(3)/(2)}`

`{k(x)}'=(7(e^x)(1+49e^(2x))(49e^(2x)-(1)/(2)))/([1+49e^(2x)]^(3))`

For Maxima or Minima

`{k(x)}'=0`

`7(e^x)(1+49e^(2x))(98e^(2x)-1)=0`

→
`e^(x)=0∨ 1+49e^(2x)=0∨98e^(2x)-1=0`

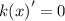
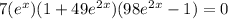
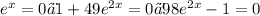
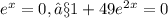`e^(x)=0  ,  ∧ 1+49e^(2x)=0` [not possible ∵there exists no value of x satisfying these equation]

→
`98e^(2x)-1=0`

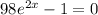
Solving this we get

x=
`-(1)/(2)ln(98)`

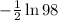
As you will evaluate
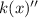`{k(x})}''`<0 at x=
`-(1)/(2)\ln98`

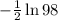
So this is the point of Maxima. we get y=7×1/√98=1/√2

(x,y)=[
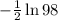`-(1)/(2)\ln98`,1/√2]

k(x)=
`\lim_(x\to\infty ) \frac{7e^(x)}{[{1+(7e^(x))^2}]^(3)/(2)}`

k(x)=
`(7)/(\infty)`

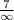
k(x)=0