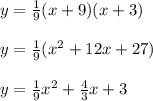Question

Write the equation of the quadratic function with roots -9 and and -3 and a vertex at (-6, -1).

Answer 1

The equation of the quadratic function is:
`y=(1)/(9)x^2+(4)/(3)x+3`

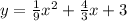
Step-by-step explanation

The two roots of the quadratic function are given as -9 and -3

So, the associative factors for those two roots will be
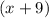`(x+9)` and
`(x+3)`

Thus, the quadratic function will be:
`y=a(x+9)(x+3)........................(1)`

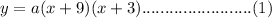
Now the vertex is at (-6, -1). As the vertex lies on the graph of this quadratic function, so that vertex point will satisfy equation (1).

So, plugging x= -6 and y = -1 into the equation (1)..........

`-1=a(-6+9)(-6+3)\\ \\ -1=a(3)(-3)\\ \\ -1=-9a\\ \\ a= (1)/(9)`

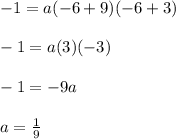
So, the quadratic function will be.....

`y=(1)/(9)(x+9)(x+3)\\ \\ y=(1)/(9)(x^2+12x+27)\\ \\ y=(1)/(9)x^2+(4)/(3)x+3`