Question

The expression (x+j)(x-j)(x-k) can be rewritten as x^3-5x^2-4x+t, where j,k, and t are constants. Which of the following is the value of t: 20, 10, -10, -20

Answer 1

The correct option is: 20

Step-by-step explanation

The expression
`(x+j)(x-j)(x-k)` can be rewritten as
`x^3-5x^2-4x+t`

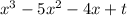
That means:
`(x+j)(x-j)(x-k)= x^3-5x^2-4x+t`

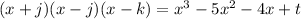
Now simplifying the left side, we will get....

`(x+j)(x-j)(x-k)= x^3-5x^2-4x+t\\ \\ (x^2-j^2)(x-k)= x^3-5x^2-4x+t\\ \\ x^3-kx^2-j^2x+j^2k= x^3-5x^2-4x+t`

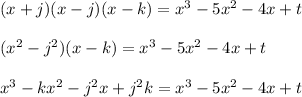
Now comparing the co-effcients of like terms in left and right side, we will get.....

`k=5, j^2=4 \\ \\ and\\ \\ t=j^2k\\ \\ So, t= (4)(5) =20`

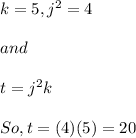
Thus, the value of 't' will be 20.