F(x) =
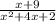
For horizontal asymptote, evaluate only the term of the numerator (top) and denominator (bottom) that has the greatest exponent. F(x) =
 .
.
**************************************************************************************
If n > m, the asymptote is: y = ∞, so asymptote does not exist
If n = m, then the asymptote is the ratio of the coefficients: y =

If n < m, then asymptote is: y =
 , so y = 0
, so y = 0
**************************************************************************************
F(x) =
 ⇒ y =
⇒ y =
 ⇒ y = 0
⇒ y = 0
Answer: y = 0