Proving a statement by contrapositive means that if you want to prove that
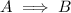 , you can instead prove that
, you can instead prove that
 since the two are equivalent.
since the two are equivalent.
So, proving that
 by contrapositive means to prove that
by contrapositive means to prove that
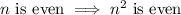
since of course the negation of being odd is being even.
This claim is quite easy to prove: if n is even, then it is twice some other integer k:
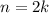
This means that its square is
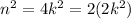
And so, if n is even, its square is also even. This proves, by contrapositive, that if n squared is odd, then n is odd.