The quadratic equation is:
 and the two values of
and the two values of
 will be 40 and 60 that will create a profit of $600.
will be 40 and 60 that will create a profit of $600.
Step-by-step explanation
The cost function is:
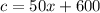 and
and
The revenue function is:

As the profit means
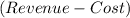 , so the Profit function will be....
, so the Profit function will be....

So, the quadratic equation is:

Now for creating a profit of $600 means, we will plug
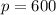 into the above equation. So.....
into the above equation. So.....

Now applying zero-product property.....
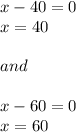
So, the two values of
 will be 40 and 60 that will create a profit of $600.
will be 40 and 60 that will create a profit of $600.