Question

A population of 550 rabbits is increasing by 2.5% each year the function y = 5.5 (1.025)× give the population of rabbits in hundreds X year from now about how long will it take the population to reach 600 rabbits? 1200 rabbits?

Answer 1

Given function : y = 5.5 (1.025)×, Where exponent x is number of years from now and y give the population of rabbits in hundreds.

We need to find the time(s) when there will be 600 rabbits and 1200 rabbits.

Solution: We know, y represents the population of rabbits in hundreds.

a) Plugging y=600 in given function, we get

600 = 5.5 (1.025)×

Dividing both sides by 5.5

600/5.5 = 5.5 (1.025)× / 5.5

600/5.5 = (1.025)×

Taking natrual log on both sides, we get

ln (600/5.5) = ln (1.025)×

ln (600/5.5) = x ln (1.025)

Dividing both sides by ln(1.05), we get

`(ln(600)/(5.5))/(ln(1.05))=x`

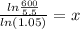
x= 96.171 years apprimately.

b) Plugging y=1200 in given function, we get

1200 = 5.5 (1.025)×

Dividing both sides by 5.5

1200/5.5 = 5.5 (1.025)× / 5.5

1200/5.5 = (1.025)×

Taking natrual log on both sides, we get

ln (1200/5.5) = ln (1.025)×

ln (1200/5.5) = x ln (1.025)

Dividing both sides by ln(1.05), we get

`(ln(1200)/(5.5))/(ln(1.05))=x`

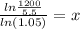
x= 110.377 years apprximately.

Therefore, it will take 96.171 years apprimately to population to reach 600 rabbits and 110.377 years approximately to population to reach 1200 rabbits.

Answer 2

Given function that shows the population of the rabbits after x years,

`y=5.5(1.025)^x-----(1)`

Where, 5.5 ( in hundred ) shows the initial population,

When the population is 600,

⇒ y = 6.6,

Then from equation (1),

`6.0=5.5(1.025)^x`

`(6)/(5.5)=(1.025)^x`

Taking log on both sides,

`log (6)/(5.5) = log (1.025)^x`

`log (6)/(5.5) = xlog (1.025)`
`(log m^n = nlog m)`

`\implies x = (log(6)/(5.5))/(log 1.025)\implies x=3.5237\approx 4`

Hence, it will take approximately 4 years to reach 600 rabbits.

Now, if the population is 1200,

⇒ y = 12,

Then from equation (1),

`12=5.5(1.025)^x`

`(12)/(5.5)=(1.025)^x`

Taking log on both sides,

`log ((12)/(55)) = log (1.025)^x`

`log ((12)/(55))= xlog (1.025)`

`\implies x = (log ((12)/(55)))/(log 1.025)\implies x=31.595\approx 32`

Hence, it will take approximately 32 years to reach 1200 rabbits.