Question

Part B- What is the equation of the line that is parallel to the line shown on the graph and goes through the point (3, 4)?

Part D- What is the equation of the line that is perpendicular to the line shown on the graph and goes through the point (-3, 2)?

Answer 1

Firstly, we will find slope of the given lne

we can select any two points from the graph

(-4,-5) and (4,-1)

so, x1=-4 , y1=-5 m x2=4 , y2=-1

now, we can use formula

`m=(y_2-y_1)/(x_2-x_1)`

now, we can plug values

`m=(-1+5)/(4+4)`

`m=(1)/(2)`

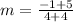
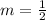
(B)

we are given

line parallel to the nline shown

and we know that

slope of two parallel lines are always equal

so, slope will also be

`m=(1)/(2)`

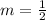
we have point as (3,4)

now, we can use point slope form of line

`y-y_1=m(x-x_1)`

we can plug values

`y-4=(1)/(2)(x-3)`

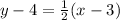
we get

`y=(1)/(2)x+(5)/(2)`

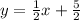
(D)

we have point as (-3, 2)

and we know that

slope of perpendicular line is -1/m

so,

`m_p=-2`

now, we can use point slope form of line

`y-2=-2(x+3)`

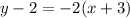
we get

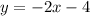`y=-2x-4`.............Answer