Question

If the parent function f(x) = x^2 is fatter translated 11 units to the left, then translated 5 units down, write the resulting function g(x) in vertex form.

a. f(x) = 1/2(x - 11)^2 - 5
b. f(x) = 1/2(x + 11)^2 - 5
c. f(x) = 2(x - 11)^2 - 5
d. f(x) = 2(x + 11)^2 - 5

If the parent function f(x) = x^2 is fatter translated 8 units to the right, then translated 1 unit down, write the resulting function g(x) in vertex form.
a. g(x) = 1/3(x - 8)^2 - 1
b. g(x) = 1/3(x + 8)^2 - 1
c. g(x) = 3(x - 8)^2 - 1
d. g(x) = 3(x + 8)^2 - 1

Answer 1

Part A.

1. If the parent function
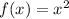`f(x) = x^2` is shrinked (looks more flattened out and fatter) with coefficient 0<k<1, then its equation is
`f(x) = kx^2.`

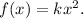
2. If the function
`f(x) = kx^2` is fatter translated 11 units to the left, then its equation becomes

`f(x) =k(x+11)^2.`

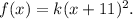
3. If the function
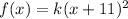`f(x) = k(x+11)^2` is translated 5 units down, then its equation becomes

`f(x) = k(x+11)^2-5` where 0<k<1.

Answer 1: correct choice is B.

Part B.

1. If the parent function
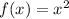`f(x) = x^2` is shrinked (looks more flattened out and fatter) with coefficient 0<k<1, then its equation is
`f(x) = kx^2.`

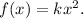
2. If the function
`f(x) = kx^2` is fatter translated 8 units to the right, then its equation becomes

`f(x) =k(x-8)^2.`

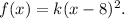
3. If the function
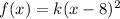`f(x) = k(x-8)^2` is translated 1 unit down, then its equation becomes

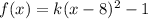`f(x) = k(x-8)^2-1` where 0<k<1.

Answer 2: correct choice is A.