Question

What is the solution of x=2+ square root x-2?

A.x = 2
B.x = 3
C.x = 2 or x = 3
D.no solution

Answer 1

So I'm going to assume that this question is asking for non extraneous solutions, or solutions that are found in the equation and are valid solutions when plugged back into the equation. So firstly, subtract 2 on both sides of the equation:

`x-2=√(x-2)`

Next, square both sides:

`(x-2)^2=x-2\\(x-2)(x-2)=x-2\\x^2-4x+4=x-2`

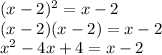
Next, subtract x and add 2 to both sides of the equation:

`x^2-5x+6=0`

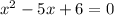
Now we are going to be factoring by grouping to find the solution(s). Firstly, what two terms have a product of 6x^2 and a sum of -5x? That would be -3x and -2x. Replace -5x with -2x - 3x:

`x^2-2x-3x+6=0`

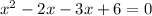
Next, factor x^2 - 2x and -3x + 6 separately. Make sure that they have the same quantity on the inside of the parentheses:

`x(x-2)-3(x-2)=0`

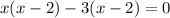
Now you can rewrite the equation as
`(x-3)(x-2)=0`

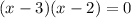
Now, apply the Zero Product Property and solve for x as such:

`x-3=0\\x=3\\\\x-2=0\\x=2`

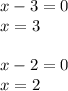
Now, it may appear that the answer is C, however we need to plug the numbers back into the original equation to see if they are true as such:

`2=2+√(2-2)\\2=2+√(0)\\2=2+0\\2=2\ \textsf{true}\\\\3=2+√(3-2)\\3=2+√(1)\\3=2+1\\3=3\ \textsf{true}`

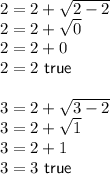
Since both solutions hold true when x = 2 and x = 3, your answer is C. x = 2 or x = 3.