Answer:
1st and 4th Option are correct.
Explanation:
Given:
A table with multiple variables.
To find: Linear relationship between variables.
First, between side length and perimeter of 1 face.
Consider,
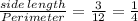
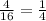
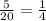
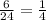
Since all the ratio are equal.
Thus, Both Variables are in Linear Relationship.
Second, between Perimeter of 1 face and Area of 1 face.
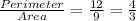
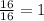
Since first two ratio are not equal.
Thus, Both Variables are not in Linear Relationship.
Third, between Surface Area and Volume
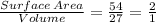
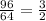
Since first two ratio are not equal.
Thus, Both Variables are not in Linear Relationship.
Fourth, between Area of 1 face. and Surface Area
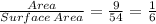
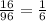
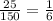
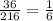
Since all the ratio are equal.
Thus, Both Variables are in Linear Relationship.
Fifth, between Side Length and Volume
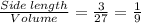
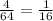
Since first two ratio are not equal.
Thus, Both Variables are not in Linear Relationship.
Therefore, 1st and 4th Option are correct.