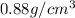Answer: The density of boat is
Step-by-step explanation:
To calculate the volume of boat, we use the equation:
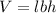
where,
V = volume of boat
l = length of boat = 2.00 cm
b = breadth of boat = 11.0 cm
h = height of boat = 11.0 cm
Putting values in above equation, we get:
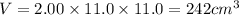
- To calculate density of a substance, we use the equation:
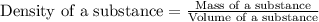
We are given:
Mass of boat = 213 g
Volume of boat =
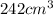
Putting values in above equation, we get:
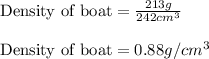
Hence, the density of boat is