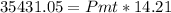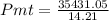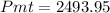Question

A man wishes to set aside some money for his son's college expenses and a graduation present. $ 8,000/yr would be drawn from the fund on the son's 18th, 19th, 20th birthday and $ 15000 will be drawn on his 21th birthday. How many dollars per year should the man deposit to the fund? The man is going to make the first deposit on his son's 5th birthday and the last on his 15th birthday. The deposits would be for equal amounts and the money in the fund compounds 5 % per year.

Answer 1

Answer: The father must deposit $2493.95.

We arrive at the answer as follows:

We start off by looking at the quantum of withdrawals and calculating their present values. The last deposit will be made when the son is 15.

Year Withdrawal Period between last Present Value @ 5%

deposit & withdrawal
`PV = (FV)/((1+r)^(n))`

---------------------------------------------------------------------------------------------------------

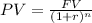
18 8000
`18-15 = 3`
`6910.70=\frac{8000}(1.05)^(3)}`

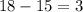
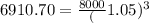
19 8000
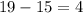`19-15 = 4` 6581.62

20 8000
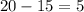`20-15 = 5` 6268.21

21 21000
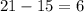`21-15 = 6` 15670.52

Total 35431.05

The total deposits at the end of year 15 should be $35431.05.

Suppose the son's 5th birthday is today. The father will make deposits of equal amounts for the next 11 years until the son's 15 years old.

We can find the value of the equal payments to be made using the Future Value of annuity formula.

`FV_(annuity) = Pmt * \left [((1+r)^(n) -1)/(r)\right ]`

Substituting the values from the equation above we get,

`35431.05= Pmt * \left [((1.05)^(11) -1)/(0.05)\right ]`

`35431.05= Pmt * \left [(1.71  -1)/(0.05)\right ]`

`35431.05= Pmt * \left [(0.71)/(0.05)\right ]`

`35431.05= Pmt * 14.21`

`Pmt =(35431.05)/(14.21)`

`Pmt = 2493.95`