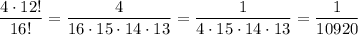You can think of the problem like this: write the cards one after the other, in a string of 16 characters. The first four characters are the cards of the first player, the next four are the cards of the second player, and so on.
So, the scenario where the first player has 4 aces is represented by the string starting with AAAA....
Since we fixed the first four places, and the next 12 are irrelevant, there are 12! combinations like these, because the other three players can have any set of four cards, we don't care.
So, there are 12! permutations that begin with four aces, and then shuffle the four kings, queens and jacks in all possible ways.
Nevertheless, these are the permutations where the first player has four aces. We must repeat this logic for all players, so there is a total of 4*12! possible scenarios in which one player has the four aces.
Finally, the total number of possible permutations is 16!, because any player can have any set of four cards.
So, the probability, computed as "good cases over all possible cases" is