Question

three adults and four children must pay $122 for tickets. Two adults and three children must pay $87. what are the price of each ticket.

Answer 1

Let
`a` be the price of an adult ticket, and
`c` the price of a child ticket.

The sentence "Three adults and four children must pay $122 for tickets" translates to
`3a+4c = 122`

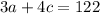
The sentence "Two adults and three children must pay $87" translates to
`2a+3c = 87`

Which leads to the linear system

`\begin{cases} 3a+4c = 122\\2a+3c = 87 \end{cases}`

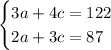
You can solve this system as you prefer, for example you can multiply the first equation by 2 and the second by 3 to get

`\begin{cases} 6a+8c = 244\\6a+9c = 261\end{cases}`

Now subtract the first from the second:

`(6a+9c) - (6a+8c) = 261-244 \iff c = 17`

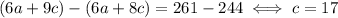
Now plug this value for c in any of the equations, for example the first:

`3a+4c = 122 \iff 3a+4\cdot 17 = 122 \iff 3a+ 68=122 \iff 3a = 54 \iff a = 18`