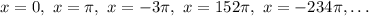Vertical asypmtotes are line of the form
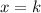 , where k is a point not in the domain of the function.
, where k is a point not in the domain of the function.
Since the definition of the cotangent function is
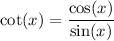
The function is not defined where the denominator is zero, i.e.
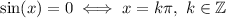
So, every line with equation
 is a vertical asymptote for the cotangent function. Some examples may be
is a vertical asymptote for the cotangent function. Some examples may be