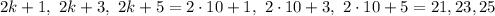Question

Three consecutive odd integers are such that the sum of the first and second is 31 less than 3 times the third. Find the integers.

Answer 1

Let the first odd integer be
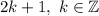`2k+1,\ k \in \mathbb{Z}`. This is a generic odd number, because 2k is twice an integer, and thus is even, and adding the +1 makes it odd.

So, three consecutive odd numbers are

`2k+1,\ 2k+3,\ 2k+5`

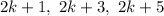
The sum of the first and second is
`2k+1 + 2k+3 = 4k+4`

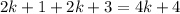
31 less than 3 times the third is
`3(2k+5)-31 = 6k-16`

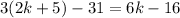
So we can define the equation

`4k+4 = 6k-16 \iff 2k = 20 \iff k = 10`

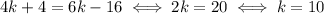
So, the three numbers are

`2k+1,\ 2k+3,\ 2k+5 = 2\cdot 10+1,\ 2\cdot 10+3,\ 2\cdot 10+5 = 21, 23, 25`