- Reflexive: no. A relation is reflexive is an element is in relation with itself. But in this case, it cannot happen, because
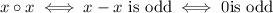 , which clearly cannot happen
, which clearly cannot happen - Symmetric: yes. A relation is symmetric if every time x and y are in relation, then also y and x are in relation. In this case, you have x and y are in relation if x-y is odd. But then, this guarantees that y and x are in relation, because
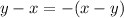 , and the opposite of an odd number is still odd
, and the opposite of an odd number is still odd - Transitive: no. A relation is transitive if every time x and y are in relation, and y and z are in relation, then x and z are in relation. So, suppose that x and y are in relation, which means
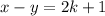 , for some integer k. We also know that y and z are in relation, which means that
, for some integer k. We also know that y and z are in relation, which means that
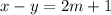 , for some integer m. But then, you have
, for some integer m. But then, you have

But since
 is twice some integer, it is even, and thus x and z are not in relation. So, we've proven that although
is twice some integer, it is even, and thus x and z are not in relation. So, we've proven that although
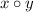 and
and
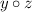 , it can't be that
, it can't be that
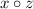 , and thus the relation is not transitive.
, and thus the relation is not transitive.