Answer:
1. 1st order chemical reaction.
2.
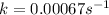 .
.
Step-by-step explanation:
Hello,
In this case, as long as the information states that when graphing the ln[cyclopropane] vs time a straight line is obtained, one infers that it is about a first order chemical reaction, this could be substantiated via the integration of the rate law:
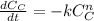
If we set n=1, we are going to obtain the aforesaid logarithm as shown below:
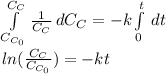
In such a way, the straight line accounts for the rate constant including the negative sign (cyclopropane's consumption), thus, the rate constant is:
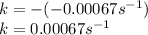
Which matches with a 1st order constant rate because of its units.
Best regards,