Question

PLEASE 25 POINTS!!!!!!

Alvin throws the football to a receiver who jumps up to catch the ball. The height of the ball over time can be represented by the quadratic equation -4.9t2 + 7.5t + 1.8 = 2.1 . This equation is based on the acceleration of gravity -4.9 m/s2, the velocity of his pass is 7.5 m/s and releases the football at a height of 1.8 meters, and the height where the receiver catches the ball of 2.1 meters. Put the equation in standard form and then solve by using the quadratic equation.

Answer 1

-4.9t²+7.5t+1.8=2.1
-4.9t²+7.5t-0.3=0

t=-7.5±√(56.25-4*-4.9*-.3)/-2*4.9

t=-7.5±√(44.49/-9.8

t=(-7.5±6.67)/-9.8

t=-.83/-9.8 = .085 or t= -14.17/-9.8 = 1.446

Answer 2

The equation in standard form is:
`-4.9t^(2) +7.5t-0.3=0`

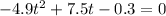
The solutions for this equation are:

t1=0.0411

t2=1.4895

Explanation:

The initial equation is:
`-4.9t^(2) +7.5t+1.8=2.1`.

The standard form of a quadratic equation is:

`a*t^(2) +b*t+c=0`.

Where a, b and c are constants, to transform the initial equation into the standard form we should subtract from both sides of the equality the number 2.1 and simplify:

`-4.9t^(2) +7.5t+1.8=2.1`

`-4.9t^(2) +7.5t+1.8 - 2.1 = 2.1 - 2.1`

`-4.9t^(2) +7.5t+1.8 - 2.1 = 0`

`-4.9t^(2) +7.5t - 0.3  = 0`

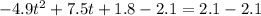
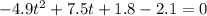
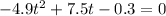
From this equation: a=-4.9, b=7.5 and c=-0.3

The solutions of a quadratic equation is given by the expressions:

`t1=\frac{-b+\sqrt[2]{b^(2)- 4*a*c} }{2*a} \\`

`t2=\frac{-b-\sqrt[2]{b^(2)- 4*a*c} }{2*a} \\`

Replacing the values of a, b and c and solving, we get:

`t1=\frac{-7.5+\sqrt[2]{7.5^(2)- 4*(-4.9)*(-0.3)} }{2*(-4.9)} \\`

t1=0.04110

`t2=\frac{-7.5-\sqrt[2]{7.5^(2)- 4*(-4.9)*(-0.3)} }{2*(-4.9)} \\`

t2=1.4895

Finally, the solutions of the quadratic equation are t1=0.04110 and t2=1.4895