Question

Suppose that we roll a red and a black die. Let a = "the black die shows a 2 or a 5", b = "the sum of the two dice is at least 7". Are events a and b independent?

Answer 1

Answer: No, A and B are not independent events.

∵ it does not satisfy the rule of probability for independent events i.e.

P(A∩B)=P(A).P(B)

Step-by-step explanation:

Let A be the event that the black dice shows 2 or 5

Let B be the event that the sum of two dice is atleast 7

Sample space of A={
`(R_1,B_2)(R_2,B_2)(R_3,B_2)(R_4,B_2)`(
`(R_5,B_2),(R_6,B_2),(R_1,B_5),(R_2,B_5),(R_3,B_5),(R_4,B_5),(R_5,B_5),(R_6,B_5)`}

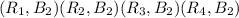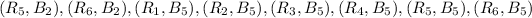Sample space of B= {
`(R_1,B_6),(R_2,B_5),(R_2,B_6),(R_3,B_4),(R_3,B_5),(R_3,B_6),`,
`(R_4,B_3),(R_4,B_4),(R_4,B_5),(R_4,B_6),(R_5,B_2),(R_5,B_3),(R_5,B_4),(R_5,B_5)`,
`(R_5,B_6),(R_6,B_2),(R_6,B_3),(R_6,B_4),(R_6,B_5),(R_6,B_5)`}

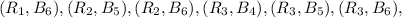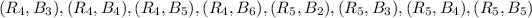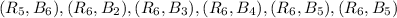P(A)=
`\frac{\text{No.of favourable outcomes}}{\text{Total no.of observation}}`

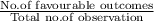
⇒P(A)=
`(12)/(36)`

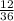
⇒P(A)=
`(1)/(3)`

Similarly,

P(B)=
`(20)/(36)`

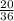
⇒ P(B) =
`(5)/(9)`

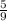
Now for Sample Space of (A∩B)= {
`(R_5,B_2)(R_6,B_2)(R_2,B_5)(R_3,B_5)(R_4,B_5)(R_5,B_5)(R_6,B_5)`}

So, P(A∩B)=
`(7)/(36)`

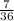
Now we apply the formula,

P(A).P(B)=P(A∩B)

`(1)/(3)`×
`(5)/(9)` ≠
`(7)/(36)`

`(5)/(27)` ≠
`(7)/(36)`

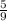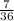
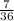
∴ The events A and B are not independent events.