Hello, UglyBruja. I've tried helping you with the problems below, and I hope this helps. If you want to solve for inequalities like these, treat them like normal equations, but don't accidentally write any equal signs.
20.)
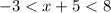
First you want x to be alone, so we can tell what it is. This means that we have to subtract 5 from both sides so that it's just x and not x + 5.
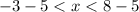
-->
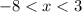
To plot this on a number line, look at how big x is. We know that x is bigger than -8, so this means you put an empty circle like this ( ° ) on the mark where it says -8, and then draw an arrow pointing to the number left of -8. since x is smaller than 3, do the same thing for the mark that says 3, but this time, make the arrow point left. Make sure your arrows never point the same direction, because then your answer will be wrong.
21.)
 or
or
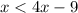
Whenever we see the word 'or' in between like that, then that means the two arrows are pointing away from each other. To solve this, we need to put the two inequalities together. But first, we need to simplify them. Let's start with the one on the left.

We need x to be alone, so subtract 2 from both sides:
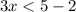
-->

Divide both sides by 3:

-->
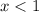
Now do the one on the right:
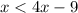
We need x to be alone, so subtract 4x from both sides.

Divide both sides by -3:
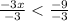
-->
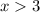
Now we know that x is bigger than 3, or smaller than 1, so mark two points: one at 3 with an arrow going right, and one at 1 with the arrow going left.
22.)
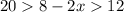
Isolate x.

-->
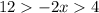
--->
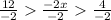
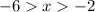 , but -6 is smaller than -2, so:
, but -6 is smaller than -2, so:
----->
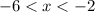
Draw a point on -6 and make the arrow go right. Then draw an arrow on -2 and make it go left.
23.)
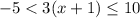
Distribute 3 to make things easier:
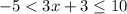
Subtract 3:

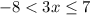
Divide by 3:
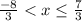
-->
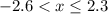
This doesn't have to be perfect, so mark a point somewhere in between -2 and -3, and make the arrow go right. Mark a point somewhere between 2 and 3. Since 2 arrows cannot point the same way, make it go left.
24.)
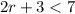 or
or
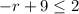
Let's simplify the one on the left.
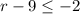
-->
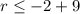
--->
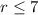
But since we switched it, then this means
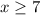
Right:
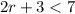
-->
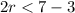
---->
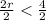
----->
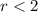
Put them together:
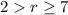
Mark a point at 2 and make the arrow go left. Mark a point at 7 and make it point right.
25.)
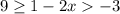
Subtract one:
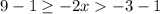
-->
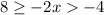
Divide by -2:
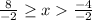
--> -4 ≥ x > 2
Mark a point at -4, make the arrow go left, mark a point at 2 and make it point right.
26.)
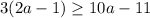
Distribute:

-->
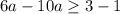
--->
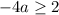
Divide both sides by 4 and a ≤
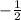
Mark a point -
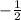 , and make the arrow go left.
, and make the arrow go left.
I hope this helped. Have a great day. : )