It is given that the height of the tower is
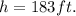
The uncertainty the measurement of this height is
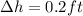
Drop time is measured as:
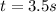
The uncertainty in measurement of time is:

Using the equation of motion:
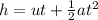 where,
where,
 is the distance covered,
is the distance covered,
 is the initial velocity,
is the initial velocity,
 is the acceleration and
is the acceleration and
 is the time.
is the time.
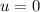 (because canon ball is in free fall). we need to calculate the value of a=g.
(because canon ball is in free fall). we need to calculate the value of a=g.
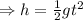
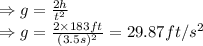
The uncertainty in this value is given by:
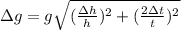
Substitute the values:
