Selling price of regular coffee = $4 per pound
Selling price of kona coffee = $11.5 per pound
Total mixture required = 20 pounds
Selling price of mixture = $6 per pound
Let quantity of regular coffee be 'a' and that of kona coffee be 'b'
⇒ Total mixture required = a + b
⇒ 20 = a + b ..................... (i)
Selling price of one pound of mixture = Price of total mixture ÷ Total pounds of mixture
⇒ 6 = [(4*a) + (11.5*b)] ÷ (a+b)
⇒ 6*a + 6*b = 4*a + 11.5*b
⇒ 2a = 5.5b
⇒ 20a = 55b
⇒ 4a = 11b
⇒ a =
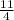 b ....................... (ii)
b ....................... (ii)
Substituting the value of (ii) in (i)
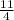 b + b = 20
b + b = 20
⇒ 11b + 4b = 20 * 4
⇒ 15b = 80
⇒ 3b = 16
⇒ b =
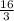
and a =
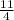 *
*
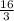
⇒ a =

So, to make the mixture we would require
 of regular coffee and
of regular coffee and
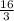 of kona coffee.
of kona coffee.