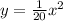Question

Find the standard form of the equation of the parabola with a focus ar (0,5) and a directrix at y=-5

Answer 1

• Vertex Form: y = a(x - h)² + k, with (h,k) as the vertex.
• How to find the "a" Variable using the Focal Length (f variable): a = 1/4f.
• Standard Form: y = ax² + bx + c
• Focal Length: The distance from the focus to the vertex.

So firstly, the focus falls on the line of symmetry (as well as the vertex) and the focus and the directrix are equidistant, or equal distance from, from the vertex. To find the focal length, take the distance from the directrix and the focus and divide it by 2.

In this case, the focus and the directrix are 10 units away, and 10 ÷ 2 = 5. 5 is your focal length.

Now, since the focus is above the directrix, this means that this is a parabola that opens up, and hence the a variable is positive. And to find the vertex, you need to subtract 5 (the focal length) from the y-coordinate of the focus:

`(0,5-5)\\(0,0)`

The vertex is (0,0). Using vertex form, plug the vertex into it:

`y=a(x-0)^2+0\\y=a(x-0)^2`

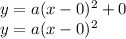
Next, we are going to find the a variable. Plug the focal length into the formula I had mentioned earlier to find it:

`(1)/(4*5)=(1)/(20)`

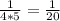
Plug 1/20 into the equation:

`y=(1)/(20)(x - 0)^2`

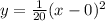
Now that we have our vertex form, we need to convert it into standard form. For this, just foil (x - 0)^2:

`y=(1)/(20)(x - 0)^2\\\\y=(1)/(20)(x - 0)(x - 0)\\\\y=(1)/(20)(x)(x)\\\\y=(1)/(20)x^2`

Your final answer is
`y=(1)/(20)x^2`