Question

Describe the continuity of the graphed function

Answer 1

The correct answer is C

Explanation:

I took the test

Answer 2

we know that

Any function f(x) is continuous at x=a only if

`\lim_(x \to a-) f(x) = \lim_(x \to a+) f(x)=f(a)`

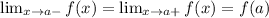
We can see that this curve is smooth everywhere except at x=3

so, we will check continuity at x=3

Left limit is:

`\lim_(x \to 3-) f(x) = -\infty`

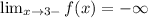
Right limit is:

`\lim_(x \to 3+) f(x) = +\infty`

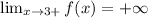
Functional value:

`f(3)= DNE`

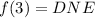
we can see that left limit is not equal to right limit

so, limit does not not exist

so, this function is discontinuous at x=3

Since, limit does not exist

so, there will be non-removal discontinuity at x=3

so, option-C........Answer