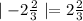Question

Help me please!!

Use the number line to determine the absolute value.
Enter the value, as a mixed number in simplest form, in the box.

Answer 1

Absolute value is just the number's distance from zero, so I beleive you just drop the negative sign. It would be 2 2/3

Answer 2

`\mid -2(2)/(3)\mid =2(2)/(3)`

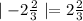
Explanation:

We are given that a number in mixed fraction

`-2(2)/(3)`

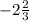
We have to find its absolute value .

Absolute value of any number :If a be number then its absolute value is given by

`\mid a\mid`

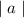
Absolute value of
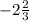`-2(2)/(3)` is given by

`\mid -2(2)/(3)\mid =2(2)/(3)`

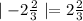
Absolute value of any number is the distance or magnitude of that number from zero on the number line.

Distance always positive.

Hence, the absolute value

`\mid -2(2)/(3)\mid =2(2)/(3)`