Question

Find a positive number that equals 42 when added to it's square

Answer 1

if the number is x, then

the positive number, when added to its square (remember, its=posessive and it's is a constraction), equals 42

this can be writen as
`x+x^2=42`

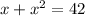
perfect, we need to solve by making one side 0 and then factoring since if ab=0, we can assume and solve for a and b by saying that a=0 and b=0

minus 42 from both sides

`x^2+x-42=0`

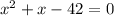
now, either use the quadratic formula or complete the square or factor

I will factor

find what 2 numbers multiply to get -42 and add to get 1 (since the linear coefient is 1 and the constant is -42)

those numbers are -6 and 7

`x^2+x-42=0`

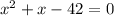
factor

`(x-6)(x+7)=0`

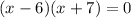
set each to 0

x-6=0

x=6

x+7=0

x=-7, false since we wanted a positive number

the number is 6