Question

Answer ASAP

What is the local maximum over the interval [–3, 1.5] for the graphed function?

0
56
–11.4
2

Answer 1

Local maximum means the maximum value of the function over the interval (-3,1.5). Since function value means y-value on graph we have to look for maximum y-value on curve which is 56 at (-1.6,56).

Hence local maximum value is 56.

Answer 2

Answer: 56 will be the maximum point for this interval.

Explanation: since maxima is a point in which a function within a range gives maximum value. And its value is called maximum value of the function over an interval.

since, we can write a function in the form of y=f(x), where y is dependent variable and x is independent variable. If that function is defined on an interval
`\left [ a, b \right ]` and for a point c, in which
`c \in (a,b)`

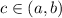
if for point c the function gives the maximum value in compare to other points then we can say that f(c) is the maximum value of function f(x) and c is the maxima of the function.

thus according to the graph it is clear that the function within the interval
`\left [ -3,1.5 \right ]` function is giving maximum value which is 56 at the point -1.6.

thus maximum value will be 56.