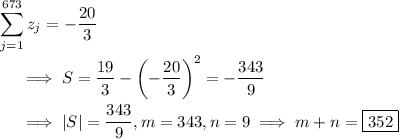Let
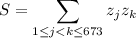
and
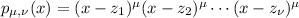
The
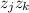 terms occur in the coefficient of the
terms occur in the coefficient of the
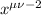 term, given by
term, given by
![\displaystyle \left[x^(\mu\\u-2)\right] p_(\mu,\\u) = \binom\mu2 \sum_(r=j)^\\u z_j^2 + \mu^2 \sum_(1 \le j < k \le \\u) z_jz_k](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vc8jordctqq7fqc2tnu8.png)
(essentially due to Vieta's formulas)
With
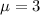 and
and
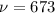 , we have
, we have
![\displaystyle \left[x^(2017)\right] p_(3,673) = \binom32 \sum_(j=1)^(673) z_j^2 + 3^2 S \\\\ ~~~~ \implies S = \frac{19}9 - \frac13 \sum_(j=1)^(673) z_j^2 \\\\ ~~~~ \implies S = \frac{19}9 - \frac13 \left(\left(\sum_(j=1)^(673) z_j\right)^2 - 2 S\right) \\\\ ~~~~ \implies S = \frac{19}3 - \left(\sum_(j=1)^(673) z_j\right)^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5ywj4jfnzhaw06uz0lr2.png)
The remaining sum on the right is the sum of the roots of
![\sqrt[3]{p_(3,673)(x)} = p_(1,673)(x)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o3y0jnjonshc2fzh0uac.png) .
.
Recall that the sum of the roots of a polynomial
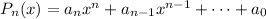
is
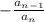 . Then the sum of the roots of
. Then the sum of the roots of
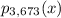 is -20, which is 3 times the sum of the roots (counting multiplicity) of
is -20, which is 3 times the sum of the roots (counting multiplicity) of
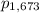 , so
, so