Question

Suppose your hair grows at the rate of 1 25 inch per day. Find the rate at which it grows in nanometers per second.

Answer 1

We just need to convert, separately, inches to (nano)meters, and days to second.

One inch is 0.0254 meters, and there are 10^9 nanometers in one meter. So, there are
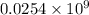`0.0254 * 10^9` nanometers in an inch.

On the other hand, one days is composed by 24 hours, each composed by 60 minutes each composed by 60 seconds. So, there are

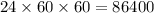`24 * 60 * 60 = 86400` seconds in a day.

Now we can perform the substitution:

`1.25 \frac{\text{inch}}{\text{day}} = 1.25* \frac{0.0254 * 10^9\text{nanometer}}{86400\text{ seconds}} = \frac{1.25*0.0254 * 10^9\text{nanometer}}{86400\text{ seconds}}`

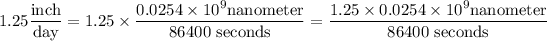
You can simplify the numeric part, getting

`1.25*0.0254 * 10^9 = 0.03175 * 10^9 = 3.175 * 10^7`

and thus

`(3.175 * 10^7)/(86400) = 0.03674768518* 10^7 = 3.674768518 * 10^5`

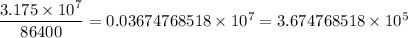
So, that's the speed, misured in nanometers per second.