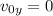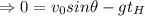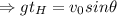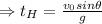Question

Find the time th it takes the projectile to reach its maximum height h. Express th in terms of v0, θ, and g (the magnitude of the acceleration d

Answer 1

An object thrown in air moving under the influence of gravitational force is known as projectile.

The projectile is thrown with an initial velocity at an angle with the horizontal. The initial velocity can be resolved in to horizontal and vertical components.

`u_(0x) = v_0 cos \theta`

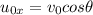
Here,
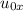`u_(0x)`is the horizontal component of initial velocity,
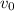`{v_0}`is the initial velocity of the projectile, and
`\theta` is the angle by which the projectile is thrown with respect to the ground.

The vertical component of initial velocity of the projectile is,

`u_(0y) = {v_0}sin \theta`

Here,
`u_(0y)` is the vertical component of initial velocity.

At maximum height the vertical velocity of the projectile momentarily goes to zero.

To calculate the time for maximum height is,

`v_(0y) = u_(0y) - gt_H`

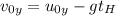
Here,
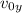`v_(0y)` is the velocity of the projectile at maximum height, g is the acceleration due to gravity, and
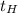`{t_H}` is the time for maximum height reached by the projectile.

Substitute
`u_(0y) = {v_0} sin\theta`

`v_(0y) = v_0 sin\theta - gt_H`

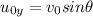
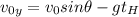
The vertical velocity at an instant at the maximum height,
`v_(0y)=0`

`\Rightarrow 0=v_0 sin\theta}-gt_H`

`\Rightarrow gt_H=v_0 sin\theta`

`\Rightarrow t_H=(v_0 sin\theta)/(g)`