Answer:
Solutions are 1.92 and -1.17
Explanation:
The general solutions of quadratic equation of the form ax²+bx+c = 0 is given by
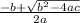 and
and
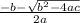
Here the the equation is 4x²-5 = 3x + 4
On rearranging
4x²-3x-5-4 = 0
4x²-3x-9 = 0
Comparing with ax²+bx+c = 0, we will get a = 4, b = -3 and c = -9
The solutions are given by
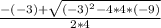 and
and
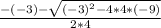
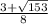 and
and
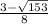
1.92 and -1.17