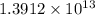Question

What number is the product of the expression below?

(2.35 x 105)(5.92 x 107)

Question 2 options:

1.3912 × 10 10


1.3912 × 10 11


1.3912 × 10 12


1.3912 × 10 13

Answer 1

`(2.35*10^5)(5.92*10^7)=(2.35\cdot5.92)(10^5\cdot10^7)\\\\=13.912\cdot10^(5+7)=13.912\cdot10^(12)=1.3912\cdot10\cdot10^(12)\\\\=\boxed{1.3912\cdot10^(13)}`

Answer 2

Answer:
`1.3912*10^(13)`

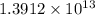
Explanation:

The given expression :
`(2.35 * 10^5)(5.92 * 10^7)`

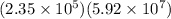
First combine the like terms (i.e. exponents together and rest of numbers together) , we get

`2.35 * 5.92 *10^5 * 10^7`

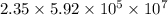
Using property ,
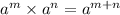`a^m* a^n=a^(m+n)` , the above repression will become

`13.912 *10^(5+7)\\\\=13.912*10^12`

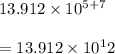
Also, in scientific form , the first number should be in decimal form where decimal should be after first digit .

Then,
`13.912*10^(12)`

`\\\\=1.3912*10*10^(12)\\\\= 1.3912*10^(1+12)\\\\=1.3912*10^(13)`

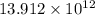
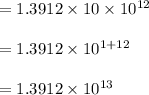
Hence, the final answer =
`1.3912*10^(13)`