Answer:
It is given that the volume of a cone =
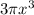 cubic units
cubic units
Volume of cone with radius 'r' and height 'h' =
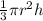
Equating the given volumes, we get
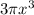 =
=
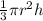

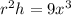
It is given that the height is 'x' units.
Therefore,
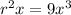
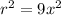
Therefore, r = 3x
So, the expression '3x' represents the radius of the cone's base in units.