Question

K is between J and M. L is between K and M. M is between K and N. If JN = 14, KM = 4, and JK = KL = LM, what is NL

Answer 1

NL=8, JK=2, KL=2, LM=2

Answer 2

NL=10 units.

Explanation:

Given information: K is between J and M. L is between K and M. M is between K and N. If JN = 14, KM = 4, and JK = KL = LM.

L is between K and M.

`KM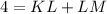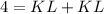=KL+LM`

`4=KL+LM` ( KM = 4)

`4=KL+KL` (KL = LM)

`4=2KL`

`2=KL`

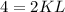
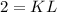
The length of KL is 2 units.

K is between J and M.

`JM=JK+KM`

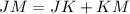
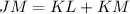`JM=KL+KM` (JK = KL)

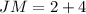`JM=2+4` (KL=2, KM=4)

`JM=6`

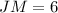
The length of JM is 6 units.

From the figure it is clear that

`MN=JN-JM`

`MN=14-6`

`MN=8`

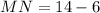
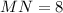
From the figure it is clear that

`NL=LM+MN`

`NL=2+8`

`NL=10`

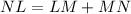
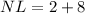
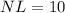
Therefore, the length of NL is 10 units.