Answer:
Maximum height of the object is 94 feet.
Maximum time taken is 2.9 seconds.
Explanation:
We have,
Height of the bridge is
 .
.
i.e.

i.e.
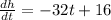
Equating
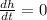 gives,
gives,
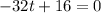
i.e.

i.e.
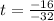
i.e.
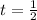
Again differentiating, we get
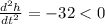 .
.
Thus, by the 'First derivative test of the maxima and minima', we get,
The maximum height of the object will be at the time,
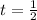 second.
second.
Thus, the maximum height is given by,
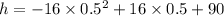
i.e.
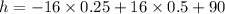
i.e.
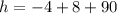
i.e.
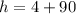
i.e. h = 94 feet.
Hence, the maximum height of the object is 94 feet.
Further, the height of the object when it reaches the ground will be 0 feet.
So, we have,
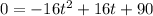
i.e.
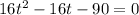
i.e.
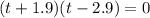
i.e. t = -1.9 sec or t = 2.9 sec
Since, time cannot be negative.
We get, the maximum time taken by the object to reach the ground is 2.9 seconds.