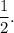Consider such events:
A - slip with number 3 is chosen;
B - the sum of numbers is 4.
You have to count
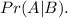
Use formula for conditional probability:
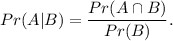
1. The event
 consists in selecting two slips, first is 3 and second should be 1, because the sum is 4. The number of favorable outcomes is exactly 1 and the number of all possible outcomes is 5·4=20 (you have 5 ways to select 1st slip and 4 ways to select 2nd slip). Then the probability of event
consists in selecting two slips, first is 3 and second should be 1, because the sum is 4. The number of favorable outcomes is exactly 1 and the number of all possible outcomes is 5·4=20 (you have 5 ways to select 1st slip and 4 ways to select 2nd slip). Then the probability of event
 is
is
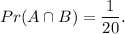
2. The event
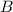 consists in selecting two slips with the sum 4. The number of favorable outcomes is exactly 2 (1st slip 3 and 2nd slip 1 or 1st slip 1 and 2nd slip 3) and the number of all possible outcomes is 5·4=20 (you have 5 ways to select 1st slip and 4 ways to select 2nd slip). Then the probability of event
consists in selecting two slips with the sum 4. The number of favorable outcomes is exactly 2 (1st slip 3 and 2nd slip 1 or 1st slip 1 and 2nd slip 3) and the number of all possible outcomes is 5·4=20 (you have 5 ways to select 1st slip and 4 ways to select 2nd slip). Then the probability of event
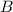 is
is
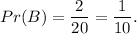
3. Then
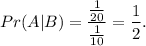
Answer: