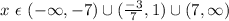Question

Solve the inequality. (Enter your answer using interval notation.)

(x(squared) + 6x − 7)/
(7x(squared) − 46x − 21)
> 0

Answer 1

`((x^2+ 6x-7))/(7x^2-46x-21) >0`

⇒
`(x^2+7x-x-7)/(7x^2-49x+3x-21) >0`

⇒
`((x-1)(x+7))/((x-7)(7x+3)) >0`

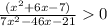
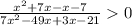
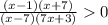
⇒ (x-1)(x+7) > 0 and (x-7)(7x+3) > 0 (In order to make the whole polynomial +ve, both numerator and denominator have to be +ve )

⇒ (x-1)>0 and (x+7)>0 or (x-1)<0 and (x+7)<0

and (either both of the polynomials are +ve or -ve)

(x-7)>0 and (7x+3)>0 or (x-7)<0 and (7x+3)<0

⇒ x > 7 , x < -7 , -3/7 < x < 1

Answer

`x \ \epsilon\ (-\infty , -7) \cup ((-3)/(7) , 1) \cup (7 , \infty)`