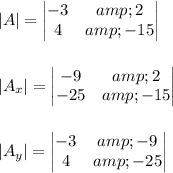Question

Which determinants can be used to solve for x and y in the system of linear equations below?

Answer 1

`\left\{\begin{array}{ccc}-3x+2y=-9\\4x-15y=-25\end{array}\right\\\\|A|=\left|\begin{array}{ccc}-3&2\\4&-15\end{array}\right|\\\\|A_x|=\left|\begin{array}{ccc}-9&2\\-25&-15\end{array}\right|\\\\|A_y|=\left|\begin{array}{ccc}-3&-9\\4&-25\end{array}\right|`

Answer 2

The determinants can be used to solve for x and y in the system of linear equations below are:

`|A|=\begin{vmatrix}-3 &2 \\ 4&-15 \end{vmatrix}\\\\\\|A_(x)|=\begin{vmatrix}-9 &2 \\ -25 &-15 \end{vmatrix}\\\\\\|A_(y)|=\begin{vmatrix}-3 &-9 \\ 4 &-25\end{vmatrix}`

Explanation:

We are given a system of linear equations as:

`-3x+2y=-9`

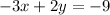
and
`4x-15y=-25`

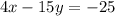
Hence, we can form a matrix with the help of these equations as:

`AX=b`

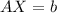
where A is a matrix formed by the coefficients of x and y and is a 2×2 matrix.

and b is a matrix formed by the term after equality and is a 2×1 matrix.

Hence, we have:

`A=\begin{bmatrix}-3 &2 \\4& -15\end{bmatrix}\\\\\\X=\begin{bmatrix}x\\y \end{bmatrix}\\\\\\b=\begin{bmatrix}-9\\ -25\end{bmatrix}`

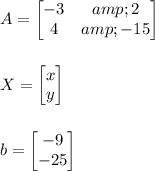
As we know that:

`x=(|A_(x)|)/(|A|)\\and\\y=(|A_(y)|)/(|A|)`

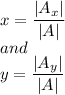
where,

`|A|=\begin{vmatrix}-3 &2 \\ 4&-15 \end{vmatrix}\\\\\\|A_(x)|=\begin{vmatrix}-9 &2 \\ -25 &-15 \end{vmatrix}\\\\\\|A_(y)|=\begin{vmatrix}-3 &-9 \\ 4 &-25\end{vmatrix}`