Answer:
The total distance traveled by the ball is
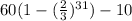
Explanation:
It is given that a certain ball is dropped from a height of x feet. It always bounces up to 2/3 x feet. So, it will form a G.P..
The ball is dropped from 10 feet. So first term of the GP is 10. The second term of the GP is
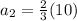
The required GP is
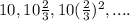
Common ratio of the GP is
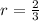
The ball stopped exactly when it touches the ground after the 30th bounce.
Since ball stopped after 30th bounce, so we need to find the sum of 31 terms.
The total distance traveled by the ball is
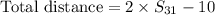
The formula for sum of n terms of a GP is
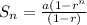
where, a is first term and r is common ratio.
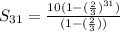
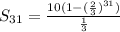
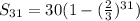
The total distance traveled by the ball is
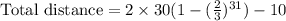
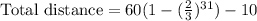
Therefore the total distance traveled by the ball is
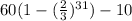 .
.