Question

Iago is interested in money. He has a collection of bills in his pocket. He finds that he has two fewer $20 bills than he does $10 bills, three more $5 bills than $10 bills, and twice as many $1 bills as $10 bills. He has a total of $160. How many of each type of bill does Iago have?

Answer 1

Let x be the number of $10 bills in Iago pocket.

1. If he has twice as many $1 bills as $10 bills, then he has (2x) $1 bills.

2. He has two fewer $20 bills than he does $10 bills, then he has (x-2) $20 bills.

3. He has three more $5 bills than $10 bills, then he has (x+3) $5 bills.

In total he has $160 that is x·10+2x·1+(x-2)·20+(x+3)·5.

Equate these two expressions and solve the equation:

`x\cdot 10+2x\cdot 1+(x-2)\cdot 20+(x+3)\cdot 5=160,\\ \\10x+2x+20x-40+5x+15=160,\\ \\37x=160+25,\\ \\37x=185,\\ \\x=5.`

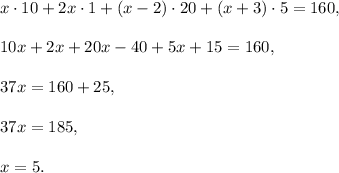
Thus, he has

• 5 bills for $10;
• 10 bills for $1;
• 3 bills for $20;
• 8 bills for $5.