Question

Points D, E, and F are collinear and DE:DF= 2/5. Point E is locate at (-3,2), point F is located at (-3,-4). What is the coordinate point of point D?

Answer 1

DE : DF = 2 : 5

So, DE = 2 parts and DF = 5 parts

EF = DF - DE

= 5 - 2

= 3 parts

DE : EF = 2 : 3

Let D be (x, y).

Then, the point E divides the line segment DF internally in the ratio 2 : 3.

So, E is
`((2(-3)+3x)/(2+3), (2(-4)+3y)/(2+3) )`

`=((3x-6)/(5), (3y-8)/(5) )`

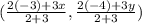
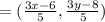
But, it is given that E is (-3, 2).

Therefore,

`(3x-6)/(5) = -3 and (3y-8)/(5)=2`

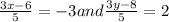
3x - 6 = -15 and 3y - 8 = 10

3x = -9 and 3y = 18

x = -3 and y = 6

Hence, D is (-3, 6)