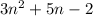Question

What is the nth term of the quadratic sequence: 6,20,40,66,98,136?

Answer 1

`3n^2+5n-2`

Explanation:

Consider the quadratic sequence : 6, 20, 40, 66, 98, 136

A quadratic sequence is of form
`an^2+bn+c`.

For n = 1 :

`6=a+b+c` ...(i)

For n = 2 :

`20=4a+2b+c` ...(ii)

For n = 3 :

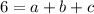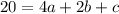`40=9a+3b+c` ...(iii)

On subtracting equation (ii) from (iii), we get

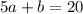`5a+b=20` ...(iv)

On subtracting equation (i) from (ii), we get

3a+b=14 ...(v)

On subtracting equation (iv) and (v) , we get

2a=6 which implies a=3

So, from equation (v), we get
`b=14-3a=14-9=5`

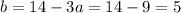
From equation (i), we get

c=6-a-b=6-3-5=-2

On putting a = 3 , b = 5, c = -2 in
`an^2+bn+c`, we get

`3n^2+5n-2`